Sulba Sutras | Baudhayana - Katyayana Sulba Sutra

The Sulba Sutras or Śulvasūtras ( शुल्बसूत्र; śulba = “string, cord, rope”, sutras = ” process or knowledge ” ) contains geometry related to fire – altar construction.

The Sulba Sutras or Vedic Geometry are part of texts called Shrauta Sutras, linked to the Vedas such as Vedic maths. They contain ancient Indian vedic math from Vedic times. Special fire-altar shapes were believed to bring gifts from Gods. The four major Shulba Sutras, attributed to Baudhayana, Manava, Apastamba, and Katyayana, are most important mathematically. They’re in old Sanskrit, likely from around 1st millennium BCE. Baudhayana’s is the oldest, possibly from 800 BCE to 500 BCE. Apastamba’s is likely next, followed by Katyayana and Manava. Katyayana came after Pāṇini’s Sanskrit codification, while Manava may be from the same time as Baudhayana.

SULBA SUTRAS served a dual purpose: they provided the guidelines for constructing sacrificial altars used in Vedic rituals and simultaneously laid the groundwork for significant mathematical discoveries. The knowledge contained within the Sulba Sutras were closely guarded and passed down orally from one generation to the next before being eventually recorded in written form.

Types of Sulba Sutras

1. Baudhayana Sulba Sutra:

Baudhayana Theorem:

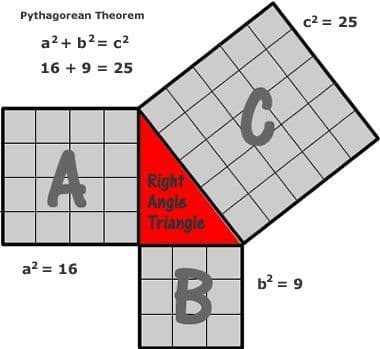
The Baudhayana Sulba Sutra contains an ancient Sanskrit verse that represents a form of the Pythagorean theorem. The verse is as follows in Sanskrit:

दीर्घचतुरश्रस्याक्ष्णयाक्ष्णया पृष्ठम् चतुरश्रश्रोन्य रज्जु: पर्यायाः ।
अद्धोवागुणाकृतोपरि ष्ठात् प्रतिष्ठाम्बौ त्रैविद्याः पृष्ठे यद्विद्यात् सोऽयं विदीयात् ॥

Transliteration: dīrghacatuśrasyākṣaṇayākṣaṇayā pṛṣṭham caturaśraśroṇya rajjuḥ paryāyāḥ | addhovāguṇākṛtopari ṣṭhāt pratiṣṭhāmbau traividyāḥ pṛṣṭhe yadvidyāt so’yaṁ vidīyāt ||

This verse presents a geometric understanding that, when translated, corresponds to a form of the Pythagorean theorem. The English translation of this verse is:

“The area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs.”

This ancient Sanskrit verse demonstrates an understanding of the relationship between the sides of a right-angled triangle and the areas of squares constructed on those sides, akin to the Pythagorean theorem.

Square Roots: Baudhayana’s Square Root Theorem expressed mathematically along with the Sanskrit formula.

Sanskrit Formula: In Sanskrit, the theorem can be expressed as follows:

यत् २ क्वर्गः (द्वयस्य वर्गमूलः) तत् अपूर्णम् सद्गुणितं द्विगुणं भाग्याद्योगेन योजयेत् ।
तत्पुनः पुनः प्रयुञ्ज्यमानमापूर्णमेकं भागं कृत्वा तस्य योजनीयम् ।
स पुनर्नवोऽपूर्णः प्रयुञ्ज्यमानः प्रयुञ्ज्यमानः नवः कुर्यादिति योगात् ।
यत्र पुनः पुनः योगयेत् तत्र सततं पुनः पुनः योगयिष्यते, तत्र तत्र सदाचलं प्राप्तं भवति ।

the English translation of the Sanskrit formula that represents Baudhayana’s Square Root Theorem:

“Where the square root of 2 (the square root of two) is incomplete, multiply it by its whole, then double the product, and with the sum add the quotient. Again, one part is to be taken of the resulting incomplete [number], and this is to be added to [the original incomplete number]. Again, this new incomplete [number] is to be multiplied by itself and the same process is to be repeated. Where this is repeatedly added again and again, there, every time it is repeatedly added, [a closer approximation] is achieved, and there, everywhere, it becomes stable.”

This Sanskrit formula reflects the iterative process for approximating the square root of 2 as described in Baudhayana’s Square Root Theorem.

In the Baudhayana sutra it appears as also:

The measure is to be increased by its third and this [third] again by its own fourth less the thirty-fourth part [of that fourth]; this is [the value of] the diagonal of a square [whose side is the measure.

which leads to the value of the square root of two as being:

Geometry Of Baudhyana:

The Baudhayana Shulba Sutra offers instructions for constructing various geometric shapes like squares and rectangles (Vedic geometry ). Additionally, it presents geometric transformations that maintain the area when changing one shape into another. These transformations include converting a square into a rectangle, an isosceles trapezium, an isosceles triangle, a rhombus, and a circle, as well as turning a circle into a square. These approximations and transformations coexist in the text, with some being more accurate than others.

1. To convert a square into a circle according to the instructions in the text, follow these steps:

Begin with a square.
Take a cord with a length equal to half the diagonal of the square.
Stretch the cord from the center of the square to the eastern side, with a portion of it extending beyond the eastern edge.
Add one-third of the portion that extends beyond the square’s eastern side to the remaining part of the half-diagonal.
Use this adjusted measurement to draw the circle you desire.

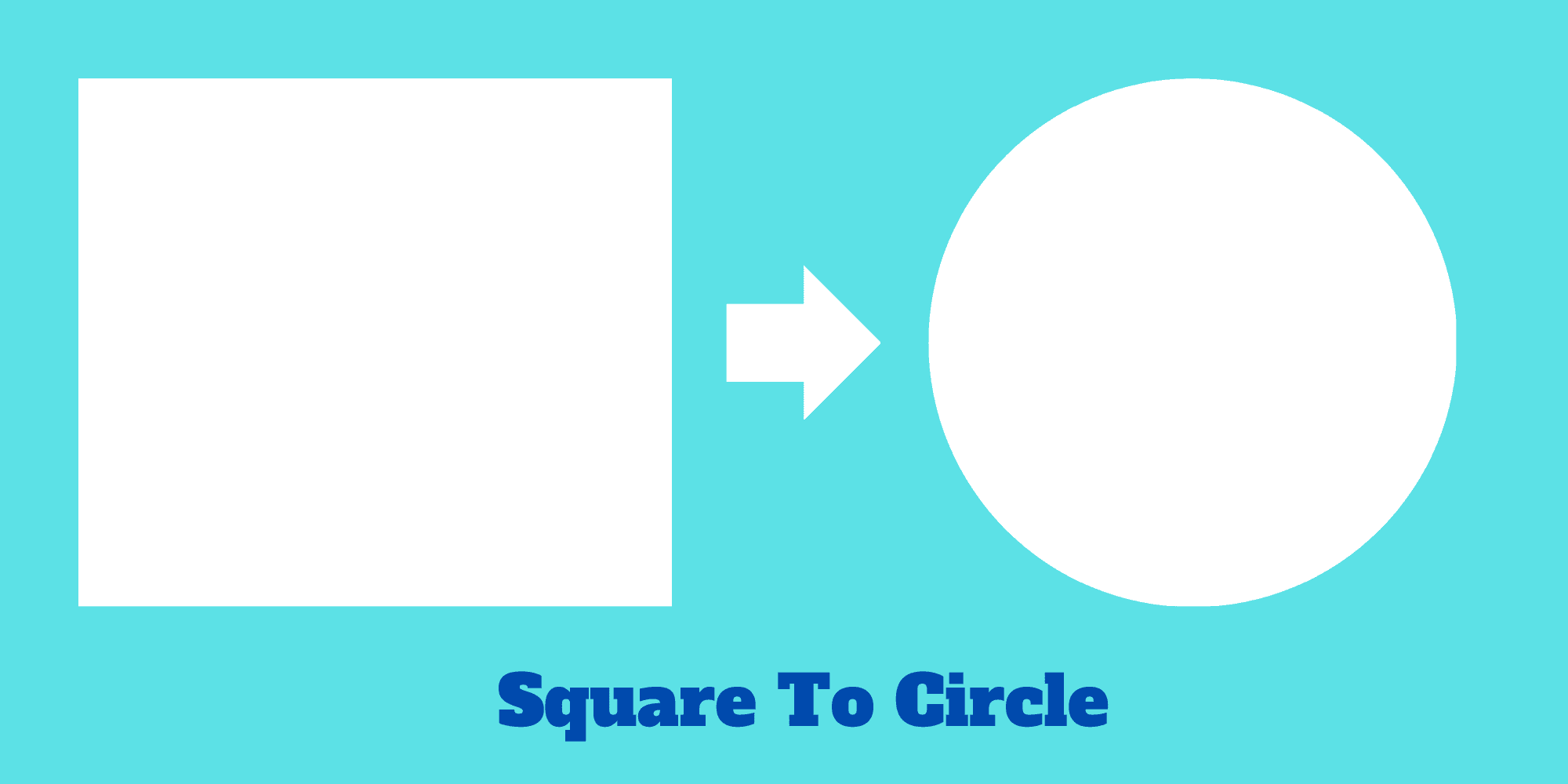
2. To convert a circle into a square following the provided instructions:

Start with a circle. Divide its diameter into eight equal parts.
Take one of these parts and divide it into twenty-nine smaller parts. Subtract twenty-eight of these smaller parts.
Additionally, subtract one-sixth of what remains after the subtraction.
Finally, subtract one-eighth of the remaining sixth part.

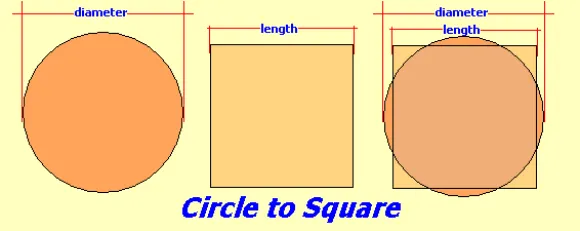
How to To convert a circle into a square

3. an alternative method to transform a circle into a square:

Begin with a circle.
Divide its diameter into fifteen equal parts.
Subtract two of these parts.
The result obtained after this subtraction is an approximation of the side length of the desired square.

2. Apastamba Sulba Sutra:

Rectangles with Equal Areas:

The Apastamba Sulba Sutra contains rules for constructing rectangles with equal areas but different dimensions. This demonstrates an understanding of algebraic principles and their application in geometry.

This can be expressed in mathematical terms as follows:

Let ‘a’ and ‘b’ be two different positive real numbers, and ‘L’ be their common multiple. To construct rectangles with equal areas using the Apastamba Sulba Sutra method, you can express it mathematically as:

Area of Rectangle 1 = a _ L Area of Rectangle 2 = b _ (L + (a/b))

Here’s the explanation:

Start with two different numbers ‘a’ and ‘b’.
Find a common multiple ‘L’ for these numbers.
Construct Rectangle 1 with sides ‘a’ and ‘L’.
Construct Rectangle 2 with sides ‘b’ and ‘L + (a/b)’.

These rectangles will have equal areas because they are derived from the same common multiple ‘L’. The Apastamba Sulba Sutra’s method ensures that the areas of these rectangles are indeed equal.

Apastamba’s rules for constructing right angles in fire-altars use the following Pythagorean triples:

(3,4,5)
(5,12,13)
(8,15,17)
(12,35,37)

3. Katyayana Sulba Sutra:

Square Roots and Fractions:

The Katyayana Sulba Sutra discusses methods for approximating square roots and dealing with fractions. While the original text does not use mathematical symbols and equations, I can provide a simplified mathematical representation of the concepts described in the Sutra:

Square Root Approximation:

Let ‘a’ be the number for which we want to approximate the square root.
The Katyayana Sulba Sutra suggests an iterative method where you repeatedly refine the approximation. Iterative Formula:
New Approximation (x_{n+1}) = Old Approximation (x_n) + (a – Old Approximation (x_n)^2) / (2 * Old Approximation (x_n))

This formula represents the iterative process for approximating the square root of ‘a’ by repeatedly refining the approximation until a satisfactory level of accuracy is achieved.

1. Dealing with Fractions:

The Sutra provides methods for adding, subtracting, multiplying, and dividing fractions using geometric and arithmetic techniques. These techniques involve using specific geometric shapes and constructions to manipulate fractions.

The Katyayana Sulba Sutra’s methods for square root approximation and handling fractions demonstrate the mathematical sophistication of ancient Indian scholars in dealing with these concepts, even though they did not use modern mathematical notation.